Important Classes - Vectors

Vektörler, bir yön ve büyüklüğü tanımlamanıza olanak tanıyan temel bir matematiksel kavramdır. Oyunlar ve uygulamalarda, vektörler genellikle bir karakterin konumu, bir nesnenin hareket hızı veya iki nesne arasındaki mesafe gibi temel özellikleri tanımlamak için kullanılır.

Vektör aritmetiği, grafik, fizik ve animasyon gibi bilgisayar programlamasının birçok yönü için temeldir ve Unity'den en iyi şekilde yararlanmak için derinlemesine anlamak faydalıdır.

Vektörler, çok boyutlu olarak ifade edilebilir ve Unity, 2D, 3D ve 4D vektörlerle çalışmak için Vector2, Vector3 ve Vector4 sınıflarını sağlar. Bu üç tür Vektör sınıfı, büyüklük gibi, birçok aynı fonksiyonu paylaşır, bu nedenle aksi belirtilmedikçe bu sayfadaki bilgilerin çoğu tüm vektör türleri için geçerlidir.

Bu sayfa, Vektör sınıflarının genel bir bakışını ve onlarla komut dosyası yazarken yaygın kullanım alanlarını sunar. Vektör sınıflarının her üyesi için kapsamlı bir referans için Vector2, Vector3 ve Vector4'ün komut dosyası referans sayfalarına bakın.

Vektör Aritmetiğini Anlamak

Toplama

İki vektör toplandığında, sonuç, orijinal vektörleri art arda "adımlar" olarak almaya eşdeğerdir. İki parametrenin sırası önemli değildir, çünkü sonuç her iki şekilde de aynıdır.

İlk vektör uzayda bir nokta olarak alınırsa, ikinci vektör bu konumdan bir offset veya "sıçrama" olarak yorumlanabilir. Örneğin, yerden 5 birim yukarıda bir nokta bulmak için şu hesaplamayı kullanabilirsiniz:-

var pointInAir = pointOnGround + new Vector2(0, 5);

Eğer vektörler kuvvetleri temsil ediyorsa, bunları yön ve büyüklük açısından düşünmek daha sezgiseldir (büyüklük, kuvvetin boyutunu belirtir). İki kuvvet vektörünün toplanması, kuvvetlerin birleşimine eşdeğer yeni bir vektörle sonuçlanır. Bu kavram, birden fazla bileşenin aynı anda etki ettiği kuvvetleri uygularken sıklıkla kullanışlıdır (örneğin, bir roket ileriye doğru itilirken aynı zamanda bir yan rüzgar tarafından etkilenebilir).

Buradaki örnekler 2D vektörleri gösterse de, aynı kavram 3D ve 4D vektörler için de geçerlidir.

Çıkarma

Vektör çıkarma, en sık bir nesneden diğerine olan yönü ve mesafeyi elde etmek için kullanılır. İki parametrenin sırası çıkarma işleminde önemlidir:-

// Vektör d, c ile aynı büyüklüğe sahiptir ancak zıt yönde işaret eder.
var c = b - a;
var d = a - b;

Sayılarla olduğu gibi, bir vektörün negatifini eklemek, pozitifini çıkarmakla aynıdır:

// Her ikisi de aynı sonucu verir.
var c = a - b;
var c = a + -b;

Bir vektörün negatifi, orijinaliyle aynı büyüklüğe sahiptir ve aynı çizgi boyunca ancak tam zıt yönde işaret eder.

Bir Nesneden Diğerine Yön ve Mesafe

Uzaydaki bir noktadan diğerini çıkardığınızda, sonuç, bir nesneden diğerine "işaret eden" bir vektördür:

// Oyuncunun konumundan hedefin konumuna işaret eden bir vektör alır.
var heading = target.position - player.position;

Bu vektör, hedef nesneye doğru işaret etmenin yanı sıra, iki konum arasındaki mesafeye eşit bir büyüklüğe sahiptir. Hedefe yön veren ancak sabit bir mesafeye sahip (örneğin bir mermiyi yönlendirmek için) "normalize edilmiş" bir vektöre ihtiyacınız olabilir. Bir vektörü kendi büyüklüğüne bölerek normalize edebilirsiniz:

var distance = heading.magnitude;
var direction = heading / distance; // Bu artık normalize edilmiş yön.

Bu yaklaşım, büyüklük ve normalize edilmiş özellikleri ayrı ayrı kullanmaktan daha iyidir, çünkü her ikisi de oldukça CPU yoğun (her ikisi de karekök hesaplamasını içerir).

Mesafeyi sadece karşılaştırma için kullanmanız gerekiyorsa (örneğin bir yakınlık kontrolü için), büyüklük hesaplamasından tamamen kaçınabilirsiniz. sqrMagnitude özelliği, büyüklük değerinin karesini verir ve büyüklük gibi hesaplanır ancak zaman alıcı karekök işlemi olmadan. Bilinen bir mesafeye karşı büyüklüğü karşılaştırmak yerine, kare büyüklüğü kare mesafeye karşılaştırabilirsiniz:-

if (heading.sqrMagnitude < maxRange * maxRange) {
    // Hedef menzil içinde.
}

Bu, karşılaştırmada gerçek büyüklüğü kullanmaktan çok daha verimlidir.

Bazen, 3D'de çalışırken, bir hedefe "yer üstü yönü" gerekebilir. Örneğin, yerde duran bir oyuncunun havada yüzen bir hedefe yaklaşması gerektiğini hayal edin. Oyuncunun konumunu hedeften çıkardığınızda, sonuç vektör hedefe doğru yukarı işaret eder. Bu, oyuncunun dönüşümünü yönlendirmek için uygun değildir; çünkü yukarı da işaret edeceklerdir; aslında gereken, oyuncunun konumundan hedefin hemen altındaki yere doğru bir vektördür. Bunu, çıkarma işleminin sonucunu alarak ve Y koordinatını sıfıra ayarlayarak elde edebilirsiniz:

var heading = target.position - player.position;
heading.y = 0; // Bu, yer üstü yönüdür.

Skaler Çarpma ve Bölme

Vektörler tartışılırken, sıradan bir sayıya (örneğin, bir float değeri) skaler denir. Bunun anlamı, bir skalerin yalnızca "ölçek" veya büyüklüğe sahip olmasıdır, oysa bir vektör hem büyüklüğe hem de yöne sahiptir.

Bir vektörü bir skalerle çarpmak, orijinal vektörle aynı yöne işaret eden bir vektörle sonuçlanır. Ancak, yeni vektörün büyüklüğü, orijinal büyüklüğün skaler değerle çarpımına eşittir.

Benzer şekilde, skaler bölme, orijinal vektörün büyüklüğünü skalerle böler.

Bu işlemler, vektör bir hareket offseti veya kuvveti temsil ettiğinde kullanışlıdır. Vektörün yönünü etkilemeden büyüklüğünü değiştirmenize olanak tanır.

Herhangi bir vektör kendi büyüklüğüne bölündüğünde, sonuç 1 büyüklüğünde bir vektördür, bu da normalize edilmiş bir vektör olarak bilinir. Eğer normalize edilmiş bir vektör bir skalerle çarpılırsa, sonucun büyüklüğü bu skaler değere eşit olacaktır. Bu, bir kuvvetin yönü sabit olduğunda ancak gücü kontrol edilebilir olduğunda kullanışlıdır (örneğin, bir arabanın tekerleğinden gelen kuvvet her zaman ileriye doğru iter ancak güç sürücü tarafından kontrol edilir).

Dot Ürünü

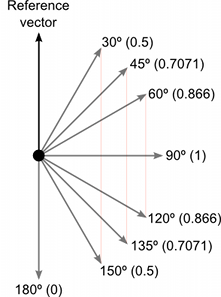
Dot ürünü, iki vektörü alır ve bir skaler döndürür. Bu skaler, iki vektörün büyüklüklerinin çarpımına ve sonuç olarak vektörler arasındaki açının kosinüsüne eşittir. Her iki vektör de normalize edildiğinde, kosinüs, ilk vektörün ikinci yönde ne kadar uzandığını (veya tam tersi - parametrelerin sırası önemli değildir) belirtir.

Aşağıda, farklı açılara sahip vektörlerin bir referans vektörle karşılaştırıldığında 1 ile -1 arasında bir dot ürünü değeri döndürdüğünü görebilirsiniz:

Dot ürünü, kosinüs hesaplamaktan daha basit bir matematiksel işlemdir, bu nedenle bazı durumlarda Mathf.Cos fonksiyonu veya vektör büyüklüğü işlemi yerine kullanılabilir (tam olarak aynı şeyi yapmaz ancak bazen etki eşdeğerdir). Ancak, dot ürünü fonksiyonunu hesaplamak çok daha az CPU süresi alır ve bu nedenle değerli bir optimizasyon olabilir.

Dot ürünü, bir vektörün büyüklüğünün ne kadarının diğer bir vektörün yönünde olduğunu hesaplamak istediğinizde kullanışlıdır.

Örneğin, bir arabanın hız göstergesi genellikle tekerleklerin dönme hızını ölçerek çalışır. Araba doğrudan ileriye doğru hareket etmiyor olabilir (örneğin, yanlamasına kayıyor olabilir), bu durumda hareketin bir kısmı arabanın baktığı yönde olmayacaktır - ve bu nedenle hız göstergesi tarafından ölçülmeyecektir. Bir nesnenin rigidbody.velocity vektörünün büyüklüğü, genel hareket yönündeki hızı verir, ancak ileri yöndeki hızı izole etmek için dot ürününü kullanmalısınız:

var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);

Doğal olarak, yön istediğiniz herhangi bir şey olabilir, ancak bu hesaplama için yön vektörü her zaman normalize edilmelidir. Sonuç, hızın büyüklüğünden daha doğru olmasının yanı sıra, büyüklüğü bulmak için gereken yavaş karekök işlemini de önler.

Çapraz Ürün

Çapraz ürün, yalnızca 3D vektörler için anlamlıdır. Girdi olarak iki 3D vektör alır ve sonucunda başka bir 3D vektör döndürür.

Sonuç vektörü, iki giriş vektörüne diktir. Çıkış vektörünün yönünü, giriş vektörlerinin sıralamasından hatırlamak için "sağ el kuralı"nı kullanabilirsiniz. Parmaklarınızı giriş vektörlerinin sırasına göre kıvırabiliyorsanız, başparmağınız çıkış vektörünün yönünü gösterir. Parametrelerin sırası tersine çevrilirse, sonuç vektörü tam zıt yönde işaret eder ancak aynı büyüklüğe sahip olur.

Sonucun büyüklüğü, giriş vektörlerinin büyüklüklerinin çarpımına ve ardından bu değerin aralarındaki açının sinüsü ile çarpımına eşittir. Sinüs fonksiyonunun bazı kullanışlı değerleri aşağıda gösterilmiştir:-

Çapraz ürün, birkaç yararlı bilgiyi dönüş değerinde birleştirdiği için karmaşık görünebilir. Ancak, dot ürünü gibi, matematiksel olarak çok verimlidir ve sinüs ve kosinüs gibi daha yavaş transandantal fonksiyonlara bağlı kodu optimize etmek için kullanılabilir.

Normal/Dik Vektör Hesaplama

Bir "normal" vektör (yani, bir düzleme dik bir vektör), mesh oluşturma sırasında sıkça gereklidir ve yol takibi ve diğer durumlarda da kullanışlıdır. Düzlemdeki üç nokta verildiğinde, örneğin bir mesh üçgeninin köşe noktaları, normali şu şekilde bulabilirsiniz: - Üç noktadan birini seçin - Her iki diğer noktadan ayrı ayrı çıkarın (iki yeni vektör, "Kenar 1" ve "Kenar 2" ile sonuçlanır) - "Kenar 1" ve "Kenar 2" vektörlerinin çapraz ürününü hesaplayın - Çapraz ürünün sonucu, üç orijinal noktanın üzerinde bulunduğu düzleme dik yeni bir vektördür - "normal".

Vector3 a;
Vector3 b;
Vector3 c;

Vector3 side1 = b - a;
Vector3 side2 = c - a;

Vector3 normal = Vector3.Cross(side1, side2);

"Sol el kuralı", çapraz ürün fonksiyonuna hangi sırayla iki vektörün geçirilmesi gerektiğine karar vermek için kullanılabilir. Yüzeyin üst tarafına (normalin dışa doğru işaret edeceği yerden) bakarken, ilk vektör saat yönünde ikinciye doğru süpürülmelidir:

Sonuç, giriş vektörlerinin sırası tersine çevrilirse tam zıt yönde işaret eder.

Mesh'ler için, normal vektör de normalize edilmelidir. Bu, normalize edilmiş özellik ile yapılabilir, ancak bazen kullanışlı olan başka bir numara vardır. Dik vektörü büyüklüğüne bölerek de normalize edebilirsiniz:-

float perpLength = perp.magnitude;
perp /= perpLength;

Başka bir yararlı not, üçgenin alanının perpLength / 2'ye eşit olduğudur. Bu, tüm ağın yüzey alanını bulmanız gerektiğinde veya göreceli alanlarına dayalı olarak üçgenleri rastgele seçmek istediğinizde kullanışlıdır.

Bu blog Unity Docs'un Türkçeye çevrilmiş halidir.